Basic HTML Version

www.geotechnicalnews.com
Geotechnical News • December 2012
35
GROUNDWATER
Hereafter, we examine only how the
time step influences the numerical
solutions, for columns with element
heights of 10, 5, 2 and 1 cm respec-
tively. Elements larger than 10 cm
were not retained because they have
been shown to yield inaccurate numer-
ical solutions in the previous steady–
state study of unsaturated seepage.
This type of problem, with a cyclic
BC, after many cycles tends towards
a cyclic stable solution having the
same period as the BC. The numerical
solutions in this short paper are only
the final solutions obtained after many
cycles.
Note that we do not know a priori
the true solution because there is no
closed–form solution to this problem.
For assessing the errors made in each
numerical solution, it is assumed
hereafter that the correct solution is
provided numerically with elements of
1 cm and time steps of 6 s.
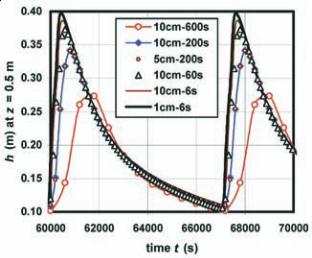
A few numerical results are given in
Figs. 3–4. It is observed first that large
time steps of 600 and 200 s provide
a poor evaluation of the periodic
variation of
h
(
z
= 0.5m) versus time
t
(Fig. 3). With the 10 cm–elements, the
peak of the hydraulic head is mark-
edly underestimated for large time
steps, but the numerical solution with
10 cm–elements and 6 s–time steps
is very close to that obtained using
1 cm–elements and 6 s–time steps.
Note also that, although the only BC
that varies with time is sinusoidal, the
response within the column is cyclic
but not sinusoidal due to the highly
non–linear properties of the unsatu-
rated soil within the column. Note also
that, for this example, using elements
of 5 cm instead of 10 cm does not
improve the numerical transient solu-
tion as shown with the case of equal
time steps of 200 s.
However, the finding may be differ-
ent for another transient problem, in
which the grid may need to be more
refined than the minimum required for
the steady–state problem being used
for initial conditions.
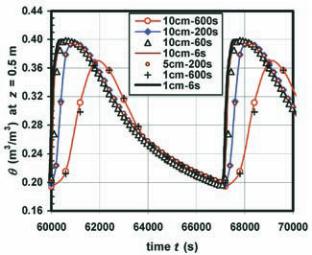
The volumetric water content
θ
at
elevation
z
= 0.5 m, versus time
t
, is
also cyclic but not sinusoidal (Fig. 4).
With the 10 cm–elements, the peak
of
θ
is underestimated for large time
steps, but the numerical solution with
time steps of 6 s is very close to that
obtained using 1 cm–elements. The
same remarks apply for Fig. 3 and Fig.
4, but the relative error on
θ
(
z
= 0.5
m,
t
) is smaller than that on
h
(
z
= 0.5
m,
t
).
A detailed study of errors is outside
the limited scope of this short paper.
When the algorithms used in a code
are known, the errors and convergence
characteristics of the finite element
equations can be studied mathemati-
cally.
Figure 1. Unsaturated functions
for volumetric water content
θ
and
hydraulic conductivity K. These
functions are used in the 1D col-
umn example.
Figure 2. Boundary condition at z =
2 m: sinus function for the hydraulic
head h versus time t.
Figure 3. The numerical solution
for h (z = 0.5 m, t) is regular for
element sizes below 10 cm (limit
provided by the steady–state study)
and approaches the correct solu-
tion when the element size and time
step are decreased. The caption
“10cm–600s” means element size
of 10 cm and time step of 600
seconds.
Figure 4. The numerical solution
for
θ
(z = 0.5 m, t) is regular for
element sizes below 10 cm (limit
provided by the steady–state study)
and approaches the correct solu-
tion when the element size and time
step are decreased.

