Geotechnical News • March 2012
33
GROUNDWATER
warning for the high aspect ratio of
20, whereas several large elements
had a size smaller than 10 m to adapt
to the problem geometry. A local view
of the finest mesh, with elements as
small as 1 cm close to the toe of the
cut-off wall and not larger than 0.5 m
elsewhere, is given in Figure 2.
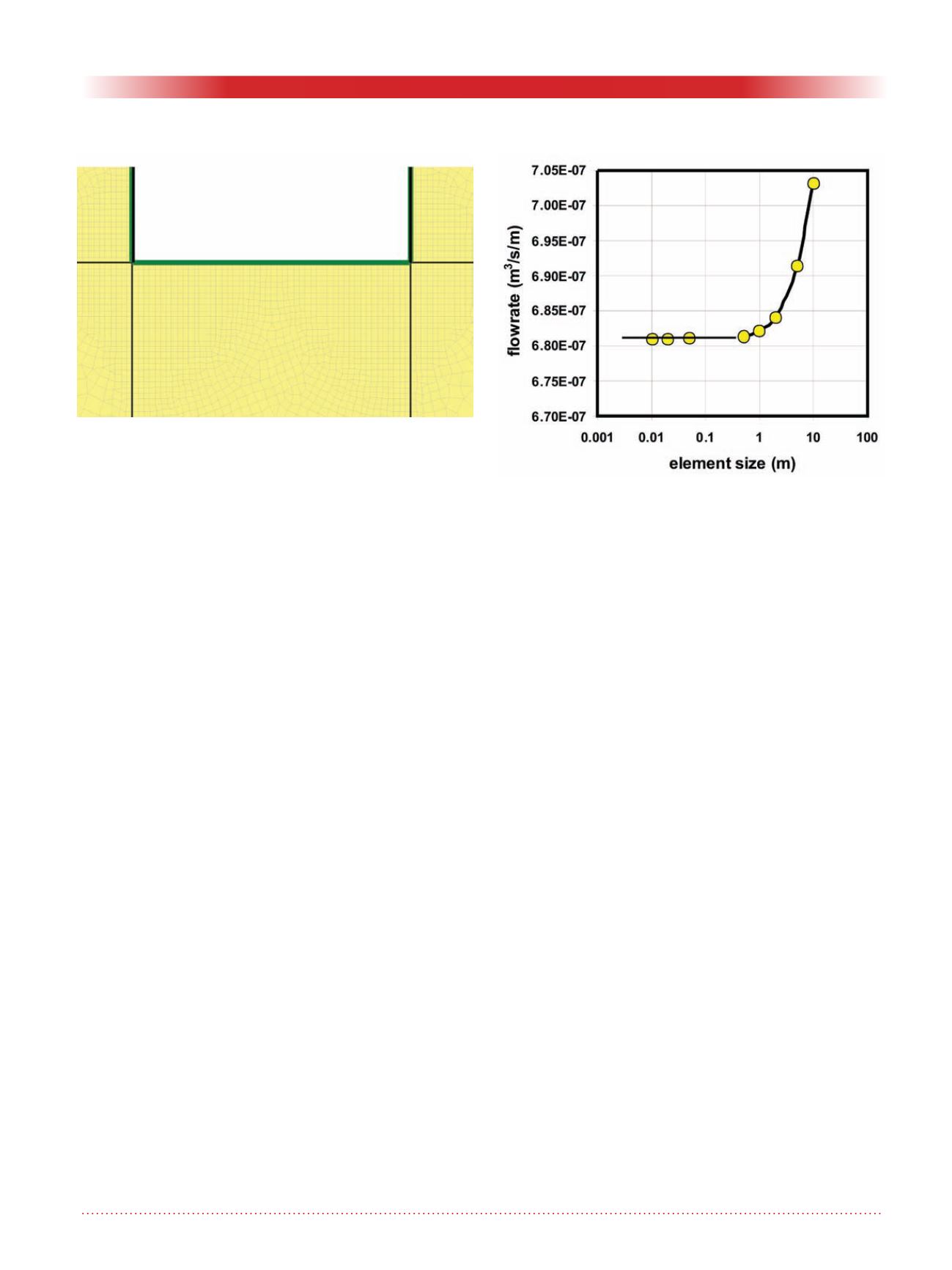
Now examine two convergence issues.
First, the leakage rate
Q
is expressed
in m
3
/s per linear meter of dam per-
pendicular to the vertical cross-section
of Figure 1. Its convergence is easily
achieved as shown in Figure 3, as soon
as the uniform element size is about 1
m. Even with a grid of 10 m, the error
on the leakage rate is only 3%. This
insensitivity to grid size explains why
it was easy, many years ago, to find
the right leakage rate using hand-
drawn flow nets.
The hydraulic gradient reaches its
maximum at the upstream angle of
the cut-off wall toe. Each time the
numerical grid is refined, this maxi-
mum gradient increases (Figure 4).
The gradient is less than unity for a
grid size greater than one metre, but
increases notably when the grid is
refined. Therefore, this is a case of
diverging maximum gradient. This
happens because the cut-off wall has
been modelled as a rectangular
impervious domain. At the upstream
and downstream toe angles, the
model induces a discontinuity in the
groundwater velocity vector, which
explains the divergence of the gradient
value. Therefore, very high hydraulic
gradients are generated locally at the
angles. This means that seepage forces
(which are proportional to the gradi-
ent), will induce local erosion (fines
are washed off), which in turn will
locally increase the soil
K
value, thus
reducing the local gradient and the
erosive action. However, this ero-
sive action at the toe could propagate
upwards, thus reducing the efficiency
of a partial cut-off wall. The risk of
local erosion at the toe explains why
it is necessary to anchor a total cut-off
toe in a solid (not likely to be eroded)
material such as bedrock.
In practice, however, a partial cut-off
wall will have a rounded toe, due to
both excavation process and erosive
action due to seepage. This rounded
toe automatically lowers the maximum
gradient, and the numerical study then
provides a convergence towards about
2 for the maximum gradient at the cut-
off wall toe.
Second example: pumping well,
confined aquifer
The second example has a closed-form
solution, which is not the case for the
first example. Therefore, in the second
example we can establish accurately
how the numerical solution converges
towards the correct closed-form solu-
tion as a function of the grid element
size.
A vertical well of radius
r
w
= 0.15 m
fully penetrates the confined aquifer
that is horizontal, homogeneous (
K
sat
=
4 x 10
-4
m/s), and of uniform thickness
b
= 2 m. The well is at the center of an
island of radius 600 m, the surround-
ing lake having a constant hydraulic
head
h
0
= 22 m. For steady-state the
hydraulic head in the well is
h
w
= 15
m, and the constant pumping rate is
Q
.
The closed-form solution is given by
the Thiem equation.
We examine here the numerically
calculated value for
Q
(m
3
/d), and
also the hydraulic head at a monitor-
ing well located at a radial distance
r
= 20.15 m. Several regular grids of
quadrilateral elements have been used.
The element size is 50 m for the coars-
est grid and 2.5 cm for the finest grid.
The numerical value of
Q
converges
towards the closed-form solution
Figure 2. Partial cut-off wall: examples of refined grid
around the toe of the cut-off wall.
Figure 3. Partial cut-off wall: Convergence of numerical
value of the leakage flowrate.


